Maths - Analysis¶
Table of Contents
Values¶
Euler number |
\(e \simeq\) 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 more e digits |
Archimedes’ constant |
\(\pi \simeq\) 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 more pi digits |
Tau as \(2\pi\) |
\(\tau \simeq\) 6.28318 53071 79586 47692 52867 66559 0057 68394 33879 87502 11641 94988 91846 15632 more tau digits |
Golden Ratio |
\(\varphi \simeq\) 1.61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 28621 35448 62270 more phi digits |
Pythagoras’ constant |
\(\sqrt 2 \simeq\) 1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799 more sqr digits |
Quadratic Function¶
Resolve the Quadratic Equation
\(ax^2+bx+c=0 \Leftrightarrow \Delta=b^2-4ac\)
\(\Delta > 0\) |
2 solutions in \(\mathbb{R}\) |
\(\frac{-b\pm\sqrt{\Delta}}{2a}\) |
\(\Delta = 0\) |
1 solution in \(\mathbb{R}\) |
\(\frac{-b}{2a}\) |
\(\Delta < 0\) |
2 solutions in \(\mathbb{C}\) |
\(\frac{-b\pm i\sqrt{-\Delta}}{2a}\) |
Remarkable Identities¶
\((a+b)^2=a^2+2ab+b^2\) |
\((a-b)^2=a^2-2ab+b^2\) |
\(a^2-b^2=(a-b)(a+b)\) |
TEMP¶
\(e^x\) |
|
|
|
\(ln(x)\) |
|
|
Cos, Sin, Tan¶
\(\theta\) \((deg)\) |
\(0\) \((0^\circ)\) |
\(\frac{\pi}{6}\) \((30^\circ)\) |
\(\frac{\pi}{4}\) \((45^\circ)\) |
\(\frac{\pi}{3}\) \((60^\circ)\) |
\(\frac{\pi}{2}\) \((90^\circ)\) |
\(\cos\) |
\(1\) |
\(\frac{\sqrt{3}}{2}\) |
\(\frac{\sqrt{2}}{2}\) |
\(\frac{1}{2}\) |
\(0\) |
\(\sin\) |
\(0\) |
\(\frac{1}{2}\) |
\(\frac{\sqrt{2}}{2}\) |
\(\frac{\sqrt{3}}{2}\) |
\(1\) |
\(\tan\) |
\(0\) |
\(\frac{\sqrt{3}}{3}\) |
\(1\) |
\(\sqrt{3}\) |
\(+\infty\) |
\(\cos^2(x)+\sin^2(x)=1\)
\(\cos(x+y)=\cos(x)*\cos(y) - \sin(x)*\sin(y)\)
\(\sin(x+y)=\sin(x)*\cos(y) + \cos(x)*\sin(y)\)
\(\cos^2(x) - \sin^2(x)=\cos(2x)\)
\(\cos^2(x) = \frac{1+\cos(2x)}{2}\)
Arccos, Arcsin, Arctan¶
\(\arcsin{0}=0\) |
\(\arccos{0}=\frac{\pi}{2}\) |
\(\arctan{0}=0\) |
\(\arcsin{\frac{3\pi}{4}}=\frac{\pi}{4}\) |
\(\arccos{-1}=\pi\) |
\(\arctan{1}=\frac{\pi}{4}\) |
\(\arcsin{-1}=-\frac{\pi}{2}\) |
\(\arccos{1}=0\) |
\(\arctan{-1}=-\frac{\pi}{4}\) |
\(\arcsin{\sin{\frac{15\pi}{4}}}=-\frac{\pi}{4}\) |
\(\arccos{\frac{-\sqrt{3}}{2}}=\frac{5\pi}{6}\) |
|
\(\arcsin{\frac{1}{2}}=\frac{\pi}{6}\) |
\(\arccos{\frac{1}{2}}=\frac{\pi}{3}\) |
Hcos, Hsin, Htan¶
\((\cosh+\sinh)(\cosh-\sinh)=1\)
\(\cosh^2(x)=\sinh^2(x)=1\)
\(\cosh(x)+\sinh(x)=e^x\)
\(\cosh(x)-\sinh(x)=e^{-x}\)
\(\cosh{x}=\frac{e^x+e^{-x}}{2}\) |
\(\arccos(\cos{x})=x [0;\pi]\) |
\(\cos(\arccos{x})=x [-1;1]\) |
\(\sinh{x}=\frac{e^x-e^{-x}}{2}\) |
\(\arcsin(\sin{x})=x [-\frac{\pi}{2};\frac{\pi}{2}]\) |
\(\sin(\arcsin{x})=x [-1;1]\) |
\(\tanh{x}=\frac{e^{2x}-1}{e^{2x}+1}\) |
\(\arctan(\tan{x})=x [-\frac{\pi}{2};\frac{\pi}{2}]\) |
\(\tan(\arctan{x})=x \mathbb{R}\) |
hyperbolic cos and sin graph
Linearisation¶
\(cos^2(x)=\frac{1-\cos{2x}}{2}\) |
\(sin^2(x)=\frac{1-\cos{2x}}{2}\) |
To develop…
Integration¶
- Derivatives
\(Function\) |
\(Derivative\) |
\(Domain\) |
|---|---|---|
\(a\) |
\(0\) |
|
\(ax\) |
\(a\) |
|
\(x^n\) |
\(nx^{n-1}\) |
|
\(\frac{1}{x^n}\) |
\(-\frac{n}{x^{n+1}}\) |
|
\(\sqrt{x}\) |
\(\frac{1}{2 \sqrt{x}}\) |
|
\(\ln{x}\) |
\(\frac{1}{x}\) |
|
\(e^x\) |
\(e^x\) |
|
\(\sin{x}\) |
\(\cos{x}\) |
|
\(\cos{x}\) |
\(-\sin{x}\) |
|
\(\tan{x}=\frac{\sin{x}}{\cos{x}}\) |
\(\frac{1}{\cos^2(x)}=1+\tan^2(x)\) |
|
\(\arcsin{x}\) |
\(\frac{1}{\sqrt{1-x^2}}\) |
|
\(\arccos{x}\) |
\(-\frac{1}{\sqrt{1-x^2}}\) |
|
\(\arctan{x}\) |
\(\frac{1}{\sqrt{1+x^2}}\) |
|
\(\sinh{x}\) |
\(\cosh{x}\) |
|
\(\cosh{x}\) |
\(\sinh{x}\) |
|
\(\tanh{x}\) |
\(\frac{1}{cosh^2(x)}\) |
|
\(ku\) |
\(ku'\) |
|
\(u+v\) |
\(u'+v'\) |
|
\(uv\) |
\(u'v+uv'\) |
|
\(\frac{u}{v}\) |
\(\frac{u'v-uv'}{v^2}\) |
|
\(u^n\) |
\(nu'u^{n-1}\) |
|
\(\sqrt{u}\) |
\(\frac{u'}{2\sqrt{u}}\) |
|
\(e^u\) |
\(u'e^u\) |
|
\(\ln{u}\) |
\(\frac{u'}{u}\) |
|
\(\arctan{u}\) |
\(\frac{u'}{1+u^2}\) |
- Primitives
\(Function\) |
\(Primitive+C\) |
\(Domain\) |
|---|---|---|
\(x^n\) |
\(\frac{1}{n+1}x^{n+1}\) |
|
\(\frac{1}{x}\) |
\(\ln{x}\) |
|
\(u'e^u\) |
\(e^u\) |
|
\(u'u^n\) |
\(\frac{1}{n+1}u^{n+1}\) |
|
\(\frac{u'}{u}\) |
\(\ln{|u|}\) |
|
\(\frac{1}{2\sqrt{x}}\) |
\(\sqrt{x}\) |
|
\(\frac{1}{\sqrt{1-u^2}}\) |
\(\arcsin{u}\) |
|
\(\frac{-1}{\sqrt{1-u^2}}\) |
\(\arccos{u}\) |
|
\(\frac{1}{1+u^2}\) |
\(\arctan{u}\) |
|
\(u'\cos{u}\) |
\(\sin{u}\) |
|
\(u'\sin{u}\) |
\(-\cos{u}\) |
|
\(\frac{u'}{\cos^2(u)}\) |
\(\tan{u}\) |
|
\(\frac{-u'}{u^2}\) |
\(\frac{1}{u}\) |
|
\(\ln{x}\) |
\(x\ln{x}-x\) |
Integration Help¶
\(x\sqrt{x} = x^{\frac{3}{2}}\)
\(\frac{1}{x^2+2x+5} = \frac{1}{(x+\alpha)(x+\beta)} \Rightarrow \frac{a}{x+\alpha}+\frac{b}{x+\beta}\)
\(\frac{1}{1+e^{-x}} = \frac{1+e^{-x}-e^{-x}}{1+e^{-x}}\)
\(\mu = \frac{1}{b-a} \int_a^b f\)
Parité: \(f(-x)=f(x)\) Paire \(f(-x)=-f(x)\) Impaire
Tangentes \(f'(a)(x-a)+f(a)=y\)
\(\lim_{x \to a} \frac{f(x)-f(a)}{x-a} = f'(a)\)
ex: \(\lim_{x \to 0} \frac{\sin{x}}{x}=\frac{\sin{x}-\sin{0}}{x-0}=\sin'(0)=\cos(0)=1\)
\((f \circ u)'(x)=u'(x)f(u(x))\)
\(f(x)=y \Leftrightarrow x=f^{-1}(y)\)
\((f^{-1})'(y)=\frac{1}{f'(x)}\) and \(y=f(x)\)
Limits¶
limits in 0
partie régulière (terme constant) => même limite => même signe
Si \(\frac{0}{0} \Rightarrow x=1+h (ex en 1) puis h \rightarrow 0\)
\(\lim\limits_{\substack{h \to 0}} ln(h) = h+\circ(h)\)
\(\lim\limits_{\substack{h \to 0}} sin(h) = h+\circ(h)\)
Integration by Parts¶
Integration by Parts Formula
\(\left\uparrow \begin{array}{l} A (arctan, arcsin, arccos) \\ L (logarithm) \\ P (polynomial) \\ E (exponential) \\ S (sin, cos, tan) \end{array}\right\} Priority (primitive)\quad Formula: \int_{a}^{b} fg' = \left[fg\right]_a^b - \int_{a}^{b} f'g\)
- Example
\(\left. \begin{array}{l} xe^x \\ u v' \end{array}\right. \left(\begin{array}{l} u=x \longrightarrow u'=1 \\v'=e^x \longrightarrow v=e^x\end{array}\right)\)
\(\int_{a}^{b} uv'=\left[uv\right]_a^b-\int_{a}^{b} u'v \Leftrightarrow ...\)
Integration by Change of Variables¶
Integration by Change of Variables
\(Formula: \int_{u(a)}^{u(b)} f(x) dx = \int_{a}^{b} f(u(t))u'(t) dt\quad\) We changed variable by posing \(x=u(t)\)
- Example
\(\int_{0}^{1} \sqrt{1-t^2}dt\) with \(t=\sin(x) \Leftrightarrow \left\{ \begin{array}{l} \frac{dt}{dx}=\cos(x) \\ dt=\cos(x) dx \end{array}\right. \left\{ \begin{array}{l} \sin{\frac{\pi}{2}}=1 \\ \sin{0}=0 \end{array}\right.\)
\(\int_{0}^{\frac{\pi}{2}} \sqrt{1-\sin^2(x)\cos(x)dx} \Leftrightarrow \int_{0}^{\frac{\pi}{2}} |\cos(x)|\cos(x)dx\)
\(Explanation: \sin^2(x)+\cos^2(x)=1 \Leftrightarrow |\cos(x)|=\sqrt{\sin^2(x)-1}\)
\(\int_{0}^{\frac{\pi}{2}} |\cos(x)|\cos(x)dx \Leftrightarrow \frac{1}{2}\left[\sin(2x)+x\right]_{0}^{\frac{\pi}{2}} = \frac{1}{2}(0+\frac{\pi}{2}-0-0)=\frac{\pi}{4}\)
\(Explanation: cos^2(x)=(\frac{e^{ix}+e^{-ix}}{2})^2 = \frac{1}{4}(e^{2ix}+e^{-2ix}+2e^{ix}e^{-ix}) = \frac{1}{2}(\cos(2x)+1)\)
Integrability and Comparison¶
\(f=\underset{\alpha}{\bigcirc}(g)\frac{f}{g}=u \underset{\alpha}{\longmapsto} \mathbb{R}>1\) |
f dominated by g |
\(f=\underset{\alpha}{\circ}(g)\frac{f}{g}=u \underset{\alpha}{\longmapsto} 0\) |
f negligible in front of g |
\(f\underset{\alpha}{\sim}(g)\frac{f}{g}=u \underset{\alpha}{\longmapsto} 1\) |
f similar to g |
- Convergence
Geometrical sequence and \(|q|<1 \rightarrow \sum_{n=0}^{+\infty} q^n = \frac{1}{1-q}\)
Real sequence with positive terms : divide by \(\frac{1}{n^2}\) or by \(\frac{2^n}{1}\)
Numerical sequence example:
\(un=\sqrt{n}-\sqrt{n-1} \Leftrightarrow \sum un =\)
\(\left. \begin{array}{l} (\sqrt{1})-\sqrt{0} \\ (\sqrt{2})-(\sqrt{1}) \\ ... \\ \sqrt{n}-(\sqrt{n-1}) \end{array}\right. = \sqrt{n} \underset{n \to +\infty}{\longmapsto} +\infty\)
\(f-g \underset{+\infty}{\longmapsto} 0 (asymptote)\)
Riemann (exponent)
\(\sum \frac{1}{n^{\alpha}}\) converges iff \(\alpha>1\)
Geometrical (reason)
\(\sum (r)^n\) converges iff \(|r|<1\)
Taylor Series¶
\(e^x = \sum\limits_{n=0}^{+\infty} \frac{x^n}{n!} = 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+...+\frac{x^n}{n!}+\circ(x^n)\)
\(\frac{1}{1-x} = \sum\limits_{n=0}^{+\infty} x^n = 1+x+x^2+x^3+...+x^n+\circ(x^n)\)
\(\ln(1+x) = \sum\limits_{n=1}^{+\infty} \frac{(-1)^{n+1}}{n}x^n = x-\frac{x^2}{2}+\frac{x^3}{3}-...+(-1)^{n-1}\frac{x^n}{n}+\circ(x^n)\)
\(\sin(x) = \sum\limits_{n=0}^{+\infty} \frac{(-1)^n}{(2n+1)!}x^{2n+1} = x-\frac{x^3}{3!}+\frac{x^5}{5!}-...+(-1)^n\frac{x^{2n+1}}{(2n)!}+\circ(x^{2n+1})\)
\(\cos(x) \sum\limits_{n=0}^{+\infty} \frac{(-1)^n}{(2n)!}x^{2n} = 1-\frac{x^2}{2!}+\frac{x^4}{4!}-...+(-1)^n\frac{x^{2n}}{(2n)!}+\circ(x^{2n})\)
\((1+x)^\alpha = 1+\sum\limits_{n=1}^{+\infty} \binom{\alpha}{n}x^n = 1+\frac{\alpha}{1!}x+\frac{\alpha(\alpha-1)}{2!}x^2+\frac{\alpha(\alpha-1)(\alpha-2}{3!}x^3+...+\frac{\alpha(\alpha-1)...(\alpha-n+1)}{n!}x^n+\circ(x^{n})\)
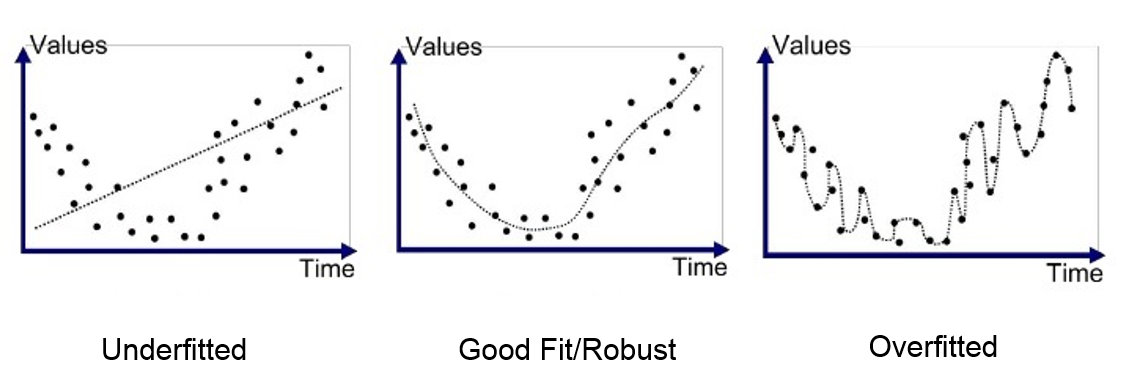
- Overfittingt and Underfitting
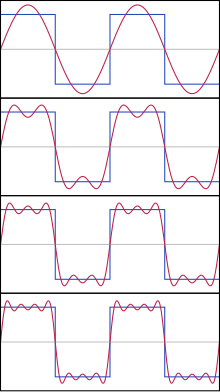
Fourier Series¶
Fourier coefficients Formula
\(\left. \begin{array}{l} an=\frac{2}{T}\int_{0}^{T} f(t)\cos(\frac{2\pi}{T}n^t)dt \\ bn=\frac{2}{T}\int_{0}^{T} f(t)\sin(\frac{2\pi}{T}n^t)dt \end{array}\right\} n \geqslant 1\)
- Fourier Transform